AI Entropy in 5 minutes
Understanding AI Temperature and why we can't just "switch randomness off".
One of the most problematic features of AI systems is their non-deterministic nature: the same input can produce slightly different outputs each time you run it.
In most software systems, this would be a bug.
This non-determinism complicates testing and general adoption, especially in safety-critical fields like 🏥 Healthcare and 🏦 Finance, where consistent, reproducible output is essential.
So why does AI behave this way? And can't we just switch the randomness off?
Let's take a look.
Temperature
Large language models like GPT generate text using a probabilistic language modelling approach. This means they produce output word by word (or token by token), each time calculating the probability of all possible next words based on the input so far.
Temperature is the parameter that adjusts how much randomness is allowed in this sampling process.
It typically ranges from 0 to 2:
At temperature = 0, the model always picks the most likely next word. This leads to fairly consistent, but often repetitive or bland output.
At temperature = 1, the model introduces moderate randomness, balancing coherence with some creativity.
At temperature > 1, the model becomes increasingly unpredictable and experimental, often at the cost of clarity or factuality.
Temperature is a setting that controls how predictable or creative a language model's output is. Lower values reduce randomness, while higher values allow more variation, creativity and surprise.
🌡️
Sadly, the Temperature setting is hardcoded in the ChatGPT UI and can only be adjusted when using OpenAI's API. The default chatGPT value is 1, it aims to balance consistency and creativity for general-purpose.
Zero Temperature
When we set the AI’s temperature setting to zero, we are signalling the model to eliminate randomness entirely, selecting only the single most likely next word at each step.
In theory, this should make the model fully deterministic, ie. the same input should always yield the same output.
But in practice, that’s not what happens!
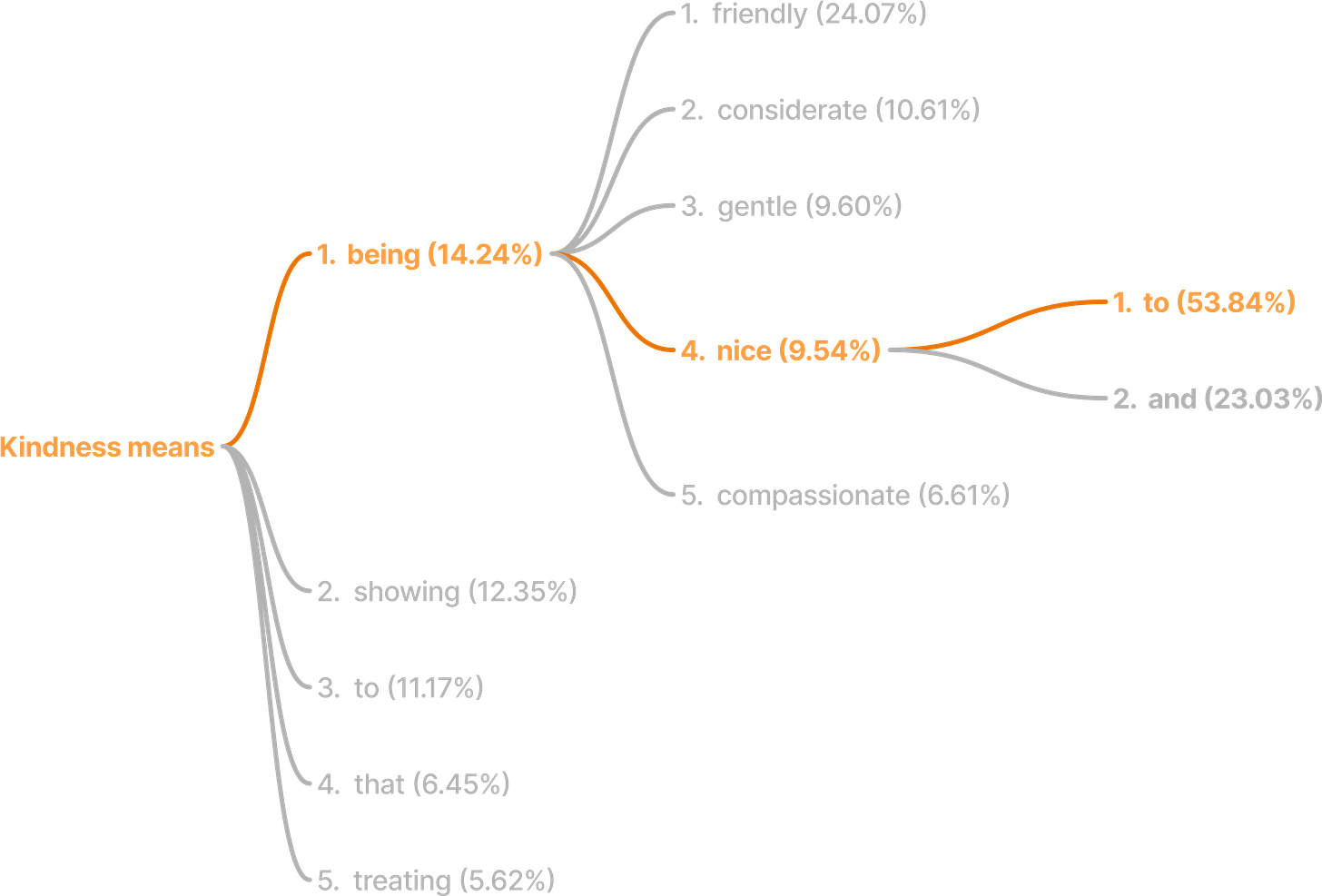
Even at Temperature=0, LLM-s return similar, but still non-deterministic responses:
The above image is the result of asking “What is kindness?“ multiple times. Although the answers start with the same few words, they quickly diverge, then take completely different paths.
Why is that?
The AI community has raised several reasons why responses can become non-deterministic, even at T=0. This article covers the top two:
Non-associativity with Parallelism
Batching
Let’s take a look at them, with some simple, non-technical explanations.
1. A drop in the Ocean
To understand the most likely cause of non-determinism, even from a non-technical perspective, imagine this story:
(It would make a great Love, Death & Robots episode!)
Imagine an evil scientist taking a drop of water from a nearby lake and dropping it into the Ocean. 🌊 +💧
We are doomed.
The ocean’s volume has changed. The sea levels have changed. Every calculation, measurement, and assumption is now wrong. We must recalculate everything!
Cartographers scramble to redraw coastlines.
Politicians from coastal nations are outraged as their countries have shrunk.
Europe and America are now separated by a slightly larger ocean, sparking diplomatic tensions over shipping lanes.
Distances must be re-measured.
Tide charts updated.
Trade routes renegotiated.
Shipping prices recalculated.
The process is so complex and so long, the world falls into chaos, and civilisation collapses. 💥
Luckily we don’t have this level of OCD. 😮💨
One drop of water, in the context of the ocean makes no measurable difference. It's entirely absorbed into the system.
This is exactly how floating-point arithmetic works in computer science.
When working with extremely large numbers, adding a very small number may have no effect at all. It simply gets swallowed by the scale of the original value.
Beyond a certain threshold, adding +1 doesn’t change the number. It’s not because the number 1 (or a drop of water) is meaningless, but because it is insignificant in the context of what it’s being added to. In other words:
A drop of water is insignificant - in the context of the Ocean. 🌊 + 💧 = 🌊
Consider the following:
🌊 + 💧 = 🌊🌊 − 🌊 = 0💧 + 💧 = 2 x 💧💧 − 💧 = 0So far so good, all of this is consistent. But here’s where things get interesting.
What is:
🌊 − 🌊 + 💧?Well, it depends how you calculate it.
If you subtract Ocean from Ocean first, you get 0 + 💧 = 💧❗️.
If you add drop to Ocean first, and then subtract Ocean, you get
🌊 − 🌊 = 0❗️
Both are correct. And both are incorrect. 🤯
This problem is known as the Nonassociativity of floating point calculation. It means that in computer science sometimes a+(b+c) ≠ (a+b)+c.
So, does this make all calculations random?
Of course not.
While non-associativity is definitely a problem, this, in itself does not cause any randomness.
However long and complex a calculation is, we can always run through it in the same order (eg left→right) and arrive at the same result.
🌊 + 💧 - 🌊 + 🌊 + 💧 + 💧 + 💧 + 🌊 − 🌊 + 💧+ 💧 - 🌊 + 🌊 = ✅
-> -> -> -> -> -> -> -> -> -> -> -> ->The problem of randomness arises, when you mix non-associativity with Parallel processing.
Parallelism
Floating-point instability becomes critical when millions of such operations happen in parallel.
Imagine a GPU trying to calculate this, by processing the small operations in parallel:
🌊 + 💧 - 🌊 + 🌊 + 💧 + 💧 + 💧 + 🌊 − 🌊 + 💧 + 💧 - 🌊 - 🌊 +
🌊 + 🌊 - 🌊 + 💧 + 💧 + 🌊 + 💧 + 🌊 − 🌊 + 🌊 + 💧 - 🌊 + 🌊 +
💧 + 💧 - 💧 - 🌊 + 🌊 - 💧 + 🌊 − 🌊 + 💧 + 💧 - 🌊 + 💧 - 🌊 +
🌊 + 🌊 - 🌊 + 🌊 + 💧 + 💧 + 🌊 − 🌊 + 💧 + 🌊 - 🌊 + 🌊 + 💧 +
🌊 + 💧 - 💧 - 🌊 + 🌊 + 🌊 + 💧 + 💧 + 🌊 + 💧 + 🌊 − 🌊 - 💧 +
💧 + 💧 - 🌊 + 💧 + 🌊 - 🌊 + 💧 - 💧 + 💧 + 🌊 − 🌊 + 🌊 + 🌊 +
💧 + 🌊 + 💧 - 🌊 + 🌊 + 🌊 + 🌊 + 💧 + 🌊 + 💧 + 💧 + 🌊 − 🌊 +
🌊 + 🌊 - 🌊 + 🌊 + 💧 - 💧 + 💧 - 🌊 − 🌊 + 💧 + 💧 - 🌊 + 🌊 +
🌊 + 🌊 - 🌊 - 🌊 + 💧 + 💧 + 💧 + 🌊 + 💧 + 🌊 − 🌊 + 💧 + 💧 = ❓ Depending on the order these parallel processes return the partial results, the final result can vary significantly.
In LLMs, that's exactly what happens. Thousands of operations (matrix multiplications, additions, layer normalisations) run simultaneously across massive compute graphs. The order of operations, the hardware used, and the precision mode (float32, float16) all affect the final outcome.
That’s why even with temperature set to zero, tiny numerical differences early in the computation can ripple through the model and produce diverging outputs.
Batching
One blog raised an alternative cause for non-determinism.
Batching, ie. processing multiple prompts simultaneously, can also cause subtle output differences.
When two or more prompts are grouped into a batch, the model processes them together. This can change internal computation paths compared to when a prompt is processed alone.
The result: even with the same prompt, you might get different answers depending on what else was in the batch.
"As a consequence, the model is no longer deterministic at the sequence-level, but only at the batch-level, as some input sequences may affect the final prediction for other inputs."
Why do LLM-s batch inputs?
Batching is a performance optimisation. It helps avoid GPU under-utilisation by ensuring parallel compute resources are kept busy, allowing large models to serve more users at once.
Mixture of Experts (MoE)
Compounding this, models like GPT-4 use a Mixture of Experts (MoE) architecture. This means that instead of using the full model for every input, only a few specialised sub-networks (called "experts") are activated based on the input.
A routing algorithm determines which experts to activate, which can introduce non-determinism: even tiny numeric differences can cause a different expert to be chosen, resulting in a completely different output trajectory.
Together, batching and MoE make high-throughput inference efficient, but they can also introduce complex, non-obvious sources of variability.
Butterfly Effect
One question that often comes up:
“Ok, so there is a 💧 change in the Ocean of context. Surely it would only change a single word or letter?”
Interestingly, no, it changes everything.
During LLM inference (ie. text generation), the smallest difference in the generated response can lead to a completely different outcome.
In language models, each word (or token) that is generated becomes part of the context used to predict the next word. This context is converted into a high-dimensional representation called an embedding. The embedding influences not only the next word, but the entire trajectory of the output that follows.
For example, changing a single word early in the response, such as "showing" instead of "being", may shift the embedding just enough to make the next prediction slightly different. That difference alters the next embedding again, and the deviation compounds with each new token.
This cascading effect, where tiny changes early on grow into major divergences later, is what makes large language models particularly sensitive to initial conditions. It's the computational equivalent of the butterfly effect. 🦋
The seed parameter
The OpenAI API also allow users to set a seed parameter. This acts like a fixed random number generator, ensuring that the same prompt produces the same output -assuming all other conditions (like temperature and model version) remain unchanged.
Sadly, just like temperature, setting a seed does not guarantee identical results. Even with a fixed seed, language models can still produce different outputs.
I tried setting a fixed seed, but within a few queries, the response text was already different. 🦋
That’s all for now!
As it stands, non-determinism is still an unsolved problem for most (if not all) large models.
As the Greek philosopher Heraclitus said:
It turns out, this wisdom is true for AI, too.
Thank you for reading!
🩵
Resources
If you are interested in Entropy in AI, I recommend reading these articles:
https://www.anyscale.com/blog/continuous-batching-llm-inference
https://medium.com/@harshit158/softmax-temperature-5492e4007f71
https://research.google/blog/mixture-of-experts-with-expert-choice-routing/?m=1
Also, some useful tech terms:
logits: raw output values produced by a model before any probability calculation. Each logit represents the model's unnormalised confidence that a specific token is the correct next word.
softmax: the function used to convert logits into a probability distribution across all tokens, modulated by temperature.
argmax: a function that selects the position of the highest value in a list, in this case, the token with the highest logit.
greedy decoding: a decoding method where the model always selects the token with the highest probability, resulting in consistent but less diverse output.
Entropy: in this context refers to the uncertainty or randomness in the model's probability distribution over the next token.
Bonus Content! ✨
Discovery of beams in T=0.
While I was playing with AI’s entropy, I did the following experiment: I asked AI: “What is Kindness” and overlayed all responses on the top of each other, so I could see the response as one long line.
Here’s what I expected:
A gradual change, where every word is more scrambled than the previous one, as the entropy keeps increasing, ie. the embeddings get more and more different between the responses.
Here’s what I got instead: 😯
A long text, starting with a block of no entropy (all texts were the same, so they were readable even after overlaying them),
followed by a block of “low entropy“, where clearly only some of the words were different
Followed by a block of “high entropy“, where the texts were completely different.
It occurred to me that this is the first time I see “Beam Search“ in action! 😍
The randomness didn’t change token-by-token, it changed beam-by-beam!
What is Beam Search?
Beam Search is a decoding strategy used in language models to find more coherent and globally optimal text sequences than greedy decoding allows.
Instead of choosing only the most likely word at each step (as in greedy decoding), Beam Search keeps track of the top N most likely sequences as the model generates each new word. These N candidates form the beam.
At each step:
The model expands each candidate sequence with all possible next tokens.
It calculates the combined score (usually log probability) for each extended sequence.
It then keeps the top N highest-scoring new sequences and discards the rest.
This continues until all sequences reach an end condition (like a stop token or max length).
By overlaying the sentences on each other from multiple responses, we can see these Beams! You can think of each Beam as an atomic “thought”, that ChatGPT forms as a unit, as part of generating a response.
I think it’s amazing.
🩵



















